教程概述
本节将简要介绍我们将在本教程中实现的 k-最近邻算法以及我们将应用该算法的 Abalone 数据集。
k-最近邻
k 最近邻算法(简称 KNN)是一种非常简单的技术。
存储整个训练数据集。当需要预测时,然后定位训练数据集中与新记录最相似的 k 条记录。从这些邻居中,可以做出总结性的预测。
记录之间的相似性可以通过多种不同的方式来衡量。可以使用特定于问题或数据的方法。一般来说,对于表格数据,欧几里得距离是一个很好的起点。
一旦发现邻居,就可以通过返回最常见的结果或取平均值来进行总结预测。因此,KNN 可用于分类或回归问题。
除了保存整个训练数据集之外,没有任何模型可言。由于在需要预测之前不会进行任何工作,因此 KNN 通常被称为惰性学习方法。
鸢尾花物种数据集
在本教程中,我们将使用鸢尾花物种数据集。
鸢尾花数据集涉及根据鸢尾花的测量来预测花的种类。
这是一个多类分类问题。每个类别的观察数量是平衡的。有 150 个观测值,包含 4 个输入变量和 1 个输出变量。变量名称如下:
- 萼片长度(厘米)。
- 萼片宽度(厘米)。
- 花瓣长度(厘米)。
- 花瓣宽度(厘米)。
- 班级
下面列出了前 5 行的示例。
|
1
2
3
4
5
6
|
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
…
|
该问题的基线性能约为 33%。
下载数据集并将其保存到当前工作目录中,文件名为“ iris.csv ”。
k-最近邻(只需 3 个简单步骤)
首先,我们将在本节中开发算法的每个部分,然后我们将在下一节中将所有元素结合在一起,形成应用于真实数据集的工作实现。
这个 k 最近邻教程分为 3 部分:
- 步骤 1:计算欧氏距离。
- 第 2 步:获取最近邻居。
- 第三步:做出预测。
这些步骤将教您实现和应用 k 最近邻算法来解决分类和回归预测建模问题的基础知识。
注意:本教程假设您使用的是 Python 3。如果您需要安装 Python 的帮助,请参阅本教程:
我相信本教程中的代码无需任何更改也适用于 Python 2.7。
第 1 步:计算欧几里德距离
第一步是计算数据集中两行之间的距离。
数据行主要由数字组成,计算两行或数字向量之间的距离的一个简单方法是画一条直线。这在 2D 或 3D 中是有意义的,并且可以很好地扩展到更高的维度。
我们可以使用欧几里得距离度量来计算两个向量之间的直线距离。它的计算方式为两个向量之间的平方差之和的平方根。
- 欧氏距离 = sqrt(i 与 N (x1_i – x2_i)^2 之和)
其中x1是第一行数据,x2是第二行数据,i是对所有列求和时特定列的索引。
对于欧氏距离,值越小,两条记录越相似。值为 0 表示两条记录之间没有差异。
下面是一个名为euclidean_distance()的函数,它在 Python 中实现了这一点。
|
1
2
3
4
5
6
|
# calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
|
您可以看到该函数假设每行的最后一列是距离计算中忽略的输出值。
我们可以用一个小的设计的分类数据集来测试这个距离函数。在构建 KNN 算法所需的元素时,我们将多次使用该数据集。
|
1
2
3
4
5
6
7
8
9
10
11
|
X1 X2 Y
2.7810836 2.550537003 0
1.465489372 2.362125076 0
3.396561688 4.400293529 0
1.38807019 1.850220317 0
3.06407232 3.005305973 0
7.627531214 2.759262235 1
5.332441248 2.088626775 1
6.922596716 1.77106367 1
8.675418651 -0.242068655 1
7.673756466 3.508563011 1
|
下面是数据集的图,使用不同的颜色来显示每个点的不同类别。
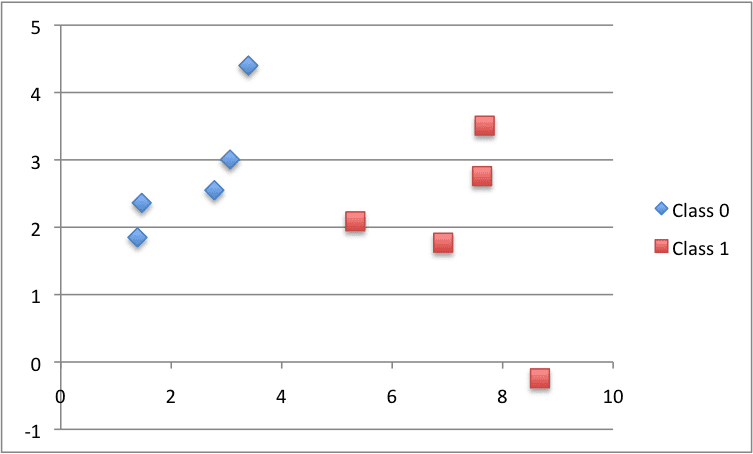
用于测试 KNN 算法的小型设计数据集的散点图
将所有这些放在一起,我们可以编写一个小示例,通过打印第一行和所有其他行之间的距离来测试我们的距离函数。我们预计第一行与其自身之间的距离为 0,这是值得留意的一件好事。
下面列出了完整的示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
# Example of calculating Euclidean distance
from math import sqrt
# calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
# Test distance function
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,–0.242068655,1],
[7.673756466,3.508563011,1]]
row0 = dataset[0]
for row in dataset:
distance = euclidean_distance(row0, row)
print(distance)
|
运行此示例将打印数据集中第一行和每一行(包括其本身)之间的距离。
|
1
2
3
4
5
6
7
8
9
10
|
0.0
1.3290173915275787
1.9494646655653247
1.5591439385540549
0.5356280721938492
4.850940186986411
2.592833759950511
4.214227042632867
6.522409988228337
4.985585382449795
|
现在是时候使用距离计算来定位数据集中的邻居了。
第 2 步:获取最近邻居
数据集中新数据的邻居是由我们的距离度量定义的k 个最接近的实例。
要在数据集中找到新数据的邻居,我们必须首先计算数据集中每个记录与新数据之间的距离。我们可以使用上面准备的距离函数来做到这一点。
计算出距离后,我们必须根据与新数据的距离对训练数据集中的所有记录进行排序。然后我们可以选择前k个作为最相似的邻居返回。
我们可以通过将数据集中每个记录的距离作为元组进行跟踪,按距离对元组列表进行排序(按降序排列),然后检索邻居来做到这一点。
下面是一个名为get_neighbors()的函数,它实现了这一点。
|
1
2
3
4
5
6
7
8
9
10
11
|
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
|
您可以看到上一步中开发的euclidean_distance()函数用于计算每个train_row和新的test_row之间的距离。
train_row和 distance 元组的列表在使用自定义键的情况下进行排序,确保在排序操作中使用元组中的第二项 ( tup[1] )。
最后,返回与test_row最相似的num_neighbors个邻居的列表。
我们可以使用上一节中准备的小型数据集来测试此函数。
下面列出了完整的示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
# Example of getting neighbors for an instance
from math import sqrt
# calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Test distance function
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,–0.242068655,1],
[7.673756466,3.508563011,1]]
neighbors = get_neighbors(dataset, dataset[0], 3)
for neighbor in neighbors:
print(neighbor)
|
运行此示例会按相似度顺序打印数据集中与第一条记录最相似的 3 个记录。
正如预期的那样,第一条记录与其自身最相似,并且位于列表的顶部。
|
1
2
3
|
[2.7810836, 2.550537003, 0]
[3.06407232, 3.005305973, 0]
[1.465489372, 2.362125076, 0]
|
现在我们知道如何从数据集中获取邻居,我们可以使用它们来进行预测。
第三步:做出预测
从训练数据集中收集的最相似的邻居可用于进行预测。
在分类的情况下,我们可以返回邻居中最具代表性的类别。
我们可以通过对邻居的输出值列表执行max()函数来实现这一点。给定在邻居中观察到的类值列表,max()函数采用一组唯一的类值,并为该组中的每个类值调用类值列表上的计数。
下面是实现此功能的名为Predict_classification()的函数。
|
1
2
3
4
5
6
|
# Make a classification prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[–1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
|
我们可以在上面设计的数据集上测试这个函数。
下面是一个完整的例子。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
# Example of making predictions
from math import sqrt
# calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a classification prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[–1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# Test distance function
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,–0.242068655,1],
[7.673756466,3.508563011,1]]
prediction = predict_classification(dataset, dataset[0], 3)
print(‘Expected %d, Got %d.’ % (dataset[0][–1], prediction))
|
运行此示例会打印预期分类 0 以及根据数据集中 3 个最相似的邻居预测的实际分类。
|
1
|
Expected 0, Got 0.
|
我们可以想象如何更改Predict_classification()函数来计算结果值的平均值。
现在我们已经具备了使用 KNN 进行预测的所有条件。让我们将其应用到真实的数据集上。
鸢尾花品种案例研究
本节将 KNN 算法应用于鸢尾花数据集。
第一步是加载数据集并将加载的数据转换为我们可以用于平均值和标准差计算的数字。为此,我们将使用辅助函数load_csv()加载文件,使用 str_column_to_float()将字符串数字转换为浮点数,使用str_column_to_int()将类列转换为整数值。
我们将使用 5 倍的 k 倍交叉验证来评估该算法。这意味着每个折叠中将包含 150/5=30 条记录。我们将使用辅助函数evaluate_algorithm()通过交叉验证来评估算法,并使用accuracy_metric()来计算预测的准确性。
开发了一个名为k_nearest_neighbors()的新函数来管理 KNN 算法的应用,首先从训练数据集中学习统计数据,然后使用它们对测试数据集进行预测。
如果您需要有关下面使用的数据加载函数的更多帮助,请参阅教程:
如果您需要有关使用交叉验证评估模型的方式的更多帮助,请参阅教程:
下面列出了完整的示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
|
# k-nearest neighbors on the Iris Flowers Dataset
from random import seed
from random import randrange
from csv import reader
from math import sqrt
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, ‘r’) as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
for i in range(len(dataset[0])):
col_values = [row[i] for row in dataset]
value_min = min(col_values)
value_max = max(col_values)
minmax.append([value_min, value_max])
return minmax
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)):
row[i] = (row[i] – minmax[i][0]) / (minmax[i][1] – minmax[i][0])
# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
dataset_split = list()
dataset_copy = list(dataset)
fold_size = int(len(dataset) / n_folds)
for _ in range(n_folds):
fold = list()
while len(fold) < fold_size:
index = randrange(len(dataset_copy))
fold.append(dataset_copy.pop(index))
dataset_split.append(fold)
return dataset_split
# Calculate accuracy percentage
def accuracy_metric(actual, predicted):
correct = 0
for i in range(len(actual)):
if actual[i] == predicted[i]:
correct += 1
return correct / float(len(actual)) * 100.0
# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
folds = cross_validation_split(dataset, n_folds)
scores = list()
for fold in folds:
train_set = list(folds)
train_set.remove(fold)
train_set = sum(train_set, [])
test_set = list()
for row in fold:
row_copy = list(row)
test_set.append(row_copy)
row_copy[–1] = None
predicted = algorithm(train_set, test_set, *args)
actual = [row[–1] for row in fold]
accuracy = accuracy_metric(actual, predicted)
scores.append(accuracy)
return scores
# Calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[–1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# kNN Algorithm
def k_nearest_neighbors(train, test, num_neighbors):
predictions = list()
for row in test:
output = predict_classification(train, row, num_neighbors)
predictions.append(output)
return(predictions)
# Test the kNN on the Iris Flowers dataset
seed(1)
filename = ‘iris.csv’
dataset = load_csv(filename)
for i in range(len(dataset[0])–1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])–1)
# evaluate algorithm
n_folds = 5
num_neighbors = 5
scores = evaluate_algorithm(dataset, k_nearest_neighbors, n_folds, num_neighbors)
print(‘Scores: %s’ % scores)
print(‘Mean Accuracy: %.3f%%’ % (sum(scores)/float(len(scores))))
|
运行该示例会打印每个交叉验证折叠的平均分类准确度分数以及平均准确度分数。
我们可以看到,平均准确度约为 96.6%,明显优于 33% 的基线准确度。
|
1
2
|
Scores: [96.66666666666667, 96.66666666666667, 100.0, 90.0, 100.0]
Mean Accuracy: 96.667%
|
我们可以使用训练数据集来预测新的观察结果(数据行)。
这涉及到调用Predict_classification()函数,其中一行代表我们的新观察结果以预测类标签。
|
1
2
3
|
...
# predict the label
label = predict_classification(dataset, row, num_neighbors)
|
我们还可能想知道预测的类标签(字符串)。
我们可以更新str_column_to_int()函数以打印字符串类名称到整数的映射,以便我们可以解释模型所做的预测。
|
1
2
3
4
5
6
7
8
9
10
11
|
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print(‘[%s] => %d’ % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
|
将它们结合在一起,下面列出了将 KNN 与整个数据集结合使用并对新观察进行单一预测的完整示例。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
|
# Make Predictions with k-nearest neighbors on the Iris Flowers Dataset
from csv import reader
from math import sqrt
# Load a CSV file
def load_csv(filename):
dataset = list()
with open(filename, ‘r’) as file:
csv_reader = reader(file)
for row in csv_reader:
if not row:
continue
dataset.append(row)
return dataset
# Convert string column to float
def str_column_to_float(dataset, column):
for row in dataset:
row[column] = float(row[column].strip())
# Convert string column to integer
def str_column_to_int(dataset, column):
class_values = [row[column] for row in dataset]
unique = set(class_values)
lookup = dict()
for i, value in enumerate(unique):
lookup[value] = i
print(‘[%s] => %d’ % (value, i))
for row in dataset:
row[column] = lookup[row[column]]
return lookup
# Find the min and max values for each column
def dataset_minmax(dataset):
minmax = list()
for i in range(len(dataset[0])):
col_values = [row[i] for row in dataset]
value_min = min(col_values)
value_max = max(col_values)
minmax.append([value_min, value_max])
return minmax
# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
for row in dataset:
for i in range(len(row)):
row[i] = (row[i] – minmax[i][0]) / (minmax[i][1] – minmax[i][0])
# Calculate the Euclidean distance between two vectors
def euclidean_distance(row1, row2):
distance = 0.0
for i in range(len(row1)–1):
distance += (row1[i] – row2[i])**2
return sqrt(distance)
# Locate the most similar neighbors
def get_neighbors(train, test_row, num_neighbors):
distances = list()
for train_row in train:
dist = euclidean_distance(test_row, train_row)
distances.append((train_row, dist))
distances.sort(key=lambda tup: tup[1])
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0])
return neighbors
# Make a prediction with neighbors
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors)
output_values = [row[–1] for row in neighbors]
prediction = max(set(output_values), key=output_values.count)
return prediction
# Make a prediction with KNN on Iris Dataset
filename = ‘iris.csv’
dataset = load_csv(filename)
for i in range(len(dataset[0])–1):
str_column_to_float(dataset, i)
# convert class column to integers
str_column_to_int(dataset, len(dataset[0])–1)
# define model parameter
num_neighbors = 5
# define a new record
row = [5.7,2.9,4.2,1.3]
# predict the label
label = predict_classification(dataset, row, num_neighbors)
print(‘Data=%s, Predicted: %s’ % (row, label))
|
运行数据首先总结类标签到整数的映射,然后在整个数据集上拟合模型。
然后定义一个新的观察(在本例中我从数据集中取出一行),并计算预测标签。
在这种情况下,我们的观察被预测为属于第一类,我们知道它是“ Iris-setosa ”
|
1
2
3
4
|
[Iris-virginica] => 0
[Iris-setosa] => 1
[Iris-versicolor] => 2
Data=[4.5, 2.3, 1.3, 0.3], Predicted: 1
|
